📘 因数分解が暗記できない？“慣れ”で得意になる3ステップ

【はじめに】

因数分解って「公式を覚えなきゃ」「パターンが多すぎる」って思われがちですが、実際は暗記じゃなくて“慣れ”の問題です。

自分自身も、公式を丸暗記したというよりは、とにかく問題を解いて、解いて、解いて……自然と“型”がしみ込んだタイプです。

でも生徒さんを見ていると、

そんな悩みを持つ子が少なくありません。

そこで今回は、因数分解を“慣れ”で得意にするための具体的な3ステップを紹介します。

【ステップ1：型別に分類して“見分け”をつける】

まずは「ごちゃ混ぜ」で練習しないことが大切です。

以下のように型ごとに分けて、10問ずつ練習してみましょう。

▼例：

・共通因数でくくるタイプ → 3x² + 6x ＝ 3x(x + 2)

・a² − b² のパターン → x² − 9 ＝ (x + 3)(x − 3)

・ax² + bx + c 型 → 2x² + 5x + 2 ＝ (2x + 1)(x + 2)

見た瞬間に「どの型か」を判断する力が育ちます。

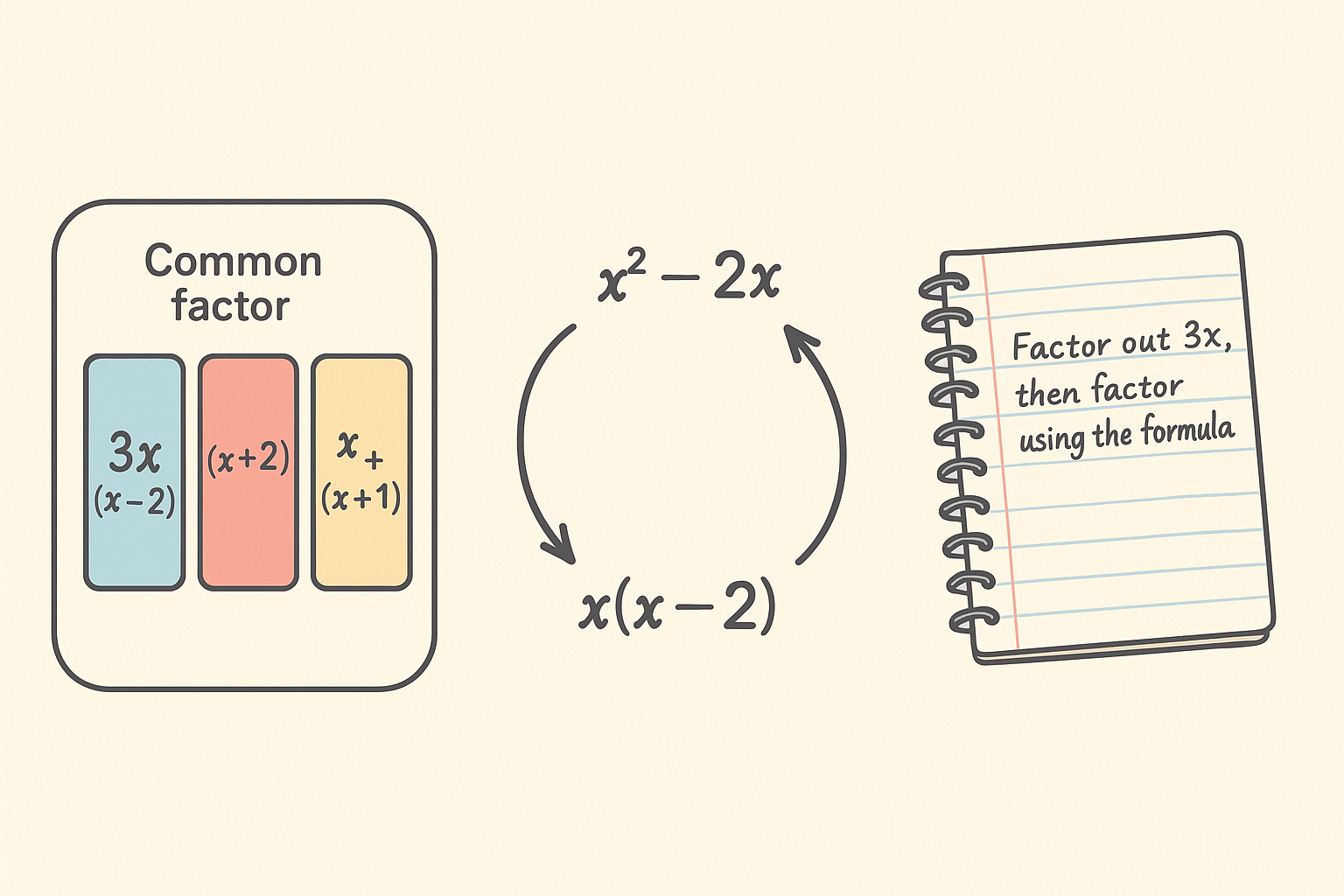
【ステップ2：展開との“往復”で構造を理解する】

「因数分解は展開の逆操作」とよく言われますが、それを実感するには“往復練習”が効果的です。

やり方は簡単。

この「行って→戻る」作業で、「なぜそうなるのか？」が腑に落ちてきます。

【ステップ3：言葉で説明してみる（言語化）】

自分で「なぜこう因数分解できるのか？」を、一言で書いてみましょう。

▼例：

「まず共通因数でくくって、そのあと公式を使って分解した」

この言語化によって、自分の思考の順序が整理され、再現性が高まります。

【まとめ：結局“慣れ”だけど、慣れ方に差がある】

因数分解が得意な子は、必ずしも暗記が得意なわけではありません。

・型に分けて練習

・展開と往復練習

・言語化の記録

この3ステップを通じて、“慣れ”を早く手に入れています。

自分も暗記ではなく、手が覚えたタイプ。

でも、今思えばこうした手順を自然と踏んでいたからこそ、得意になったんだと実感しています。