確率の基礎判断法：問題文から「順列」「組合せ」を見抜くシンプル思考法【完全版】

1. はじめに

「確率の問題を読んでも、何を使えばいいかわからない…」

これは多くの高校生が抱える共通の悩みです。

特に、順列（P）と組合せ（C）、そしてそれらの重複版の使い分けで迷うケースは非常に多いです。

原因は「公式の暗記」に偏って、判断の順番や文章の読み取り方を練習していないこと。

この記事では、基礎の基礎からスタートし、どの条件を使えば良いのかを一発で見抜く方法を、例題・注意点・練習問題付きで解説します。

最後まで読めば、点で覚えていた知識が「線」でつながります。

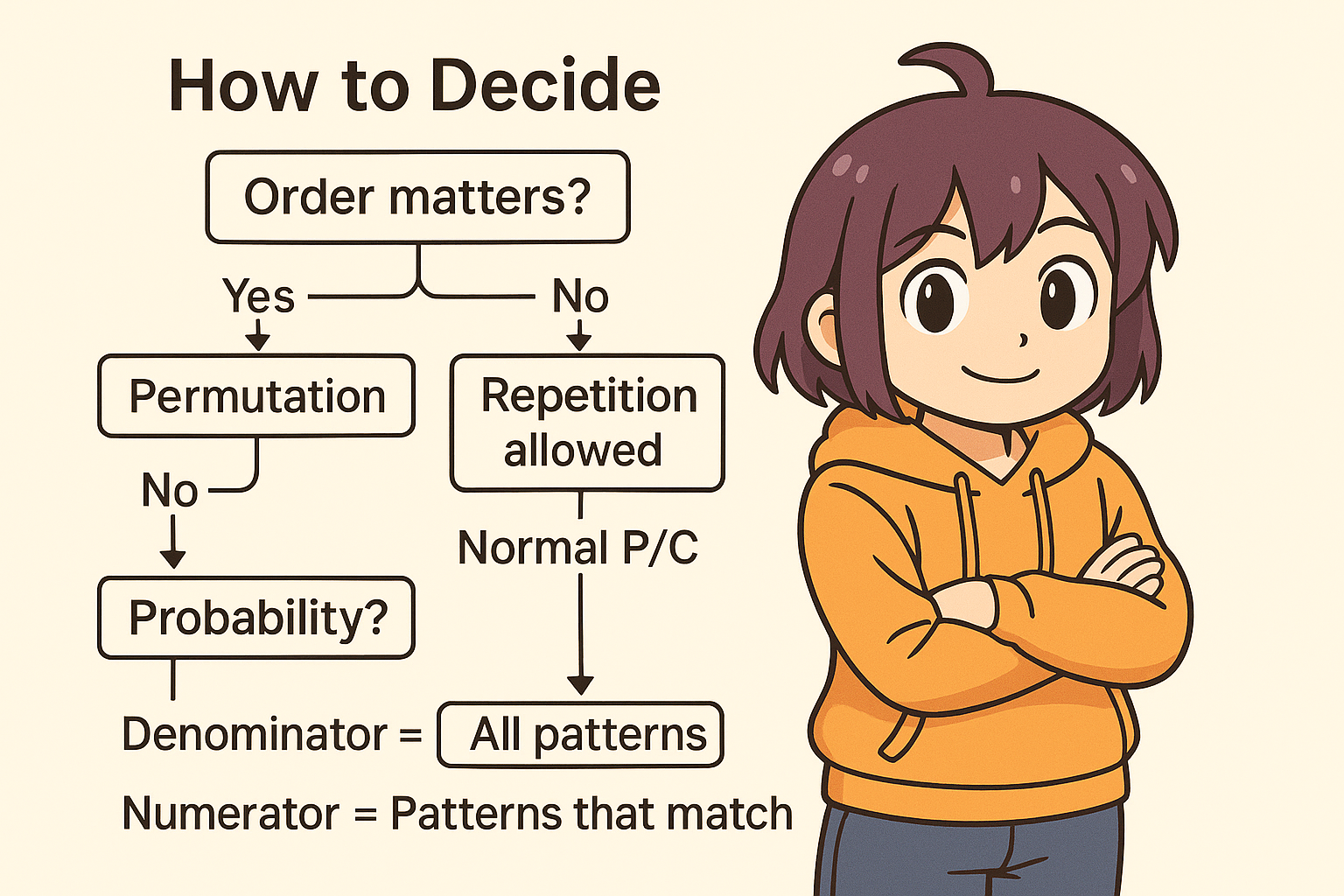
2. 判断フロー

ステップ1：順番を気にするか？

　◎ 順番が関係ある → 順列（P）

　　例：「並べる」「順位をつける」「順番を決める」「整列させる」など

　◎ 順番が関係ない → 組合せ（C）

　　例：「選ぶ」「取り出す」「グループを作る」「チーム編成」など

ステップ2：同じものを使えるか？

　◎ 同じものOK → 重複順列または重複組合せ

　　例：「同じカードを何回でも使える」「同じ数字も選べる」

　◎ 同じものNG → 普通の順列・組合せ

ステップ3：確率かどうか

　◎ 「…の確率」と聞かれている場合

　　1. 分母＝全体のパターン数（順列または組合せで求める）

　　2. 分子＝条件を満たすパターン数（同様に計算）

3. キーワード一覧

1️⃣順列（P）になりやすい言葉

　◎ 並べる

　◎ 順番を決める

　◎ 順位をつける

　◎ 列に並べる

　◎ 座席を決める

2️⃣組合せ（C）になりやすい言葉

　◎ 選ぶ

　◎ グループを作る

　◎ 抜き出す

　◎ 取り出す

　◎ チームを編成する

3️⃣重複ありのサイン

　◎ 同じものを何回でも使える

　◎ 同じ数字を選んでも良い

　◎ 「元に戻す」「戻してもう一度」

4. 基礎例題

◎ 例題1

　「5人から3人を選び、順番に並べる方法は何通りか」

　→ 選ぶ＋順番を決める → 順列

　計算：5P3 = 5×4×3 = 60通り

◎ 例題2

　「5人から3人を選ぶ方法は何通りか」

　→ 選ぶだけ（順番なし） → 組合せ

　計算：5C3 = (5×4×3) ÷ (3×2×1) = 10通り

◎ 例題3

　「1〜6の数字から2個を選び、同じ数字もOK。順番は関係なし」

　→ 同じ数字OK＋順番なし → 重複組合せ

　計算：(6+2-1)C2 = 7C2 = (7×6) ÷ (2×1) = 21通り

5. 間違えやすいパターン集

◎ 順番の有無を見落とす

◎ 重複の有無を見落とす

◎ 確率の分母を勘違いする

◎ 公式だけ覚えて文章を読まない

6. 練習問題＋解答解説

◎ 問題1

　8人から会長・副会長・会計を決める方法は何通りか。

　【解説】役職が3つあり、順番がある → 順列

　計算：8P3 = 8×7×6 = 336

　【答え】336通り

◎ 問題2

　8人から3人を選んでバレーボールのチームを作る方法は何通りか。

　【解説】順番なし、同じ人を複数回選ばない → 組合せ

　計算：8C3 = (8×7×6) ÷ (3×2×1) = 56

　【答え】56通り

◎ 問題3

　1〜5の数字から2個を選び、同じ数字もOKの場合は何通りか。

　【解説】順番なし、同じ数字OK → 重複組合せ

　計算：(5+2-1)C2 = 6C2 = (6×5) ÷ (2×1) = 15

　【答え】15通り

◎ 問題4

　1〜5の数字から2個を選んだとき、和が7になる確率は？

　【解説】

　1. 全体のパターン数：5C2 = (5×4) ÷ (2×1) = 10通り

　2. 和が7になる組：(2,5), (3,4) → 2通り

　3. 確率＝2 ÷ 10 = 1/5

　【答え】1/5

7. まとめ

◎ 「順番が関係ある？」→ Yesなら順列、Noなら組合せ

◎ 「同じもの使える？」→ Yesなら重複、Noなら普通のP/C

◎ 確率は「分母＝全体」「分子＝条件」で計算

◎ 動詞や条件をキーワードとして拾う習慣をつける