グラフと式の関係を考える!
みなさん、お久しぶりです。梅雨も明けて夏がやっと始まったような感じですね!勉強していても水分は失われていくので、たとえ冷房が効いていてもこまめな水分補給を心がけましょう。
さて、本日はオリジナル問題に挑戦してもらいます。どちらかと言うと、クイズのほうに近いので、肩の力を抜いて気楽に解いてみてください。
まずはこちらをご覧ください。
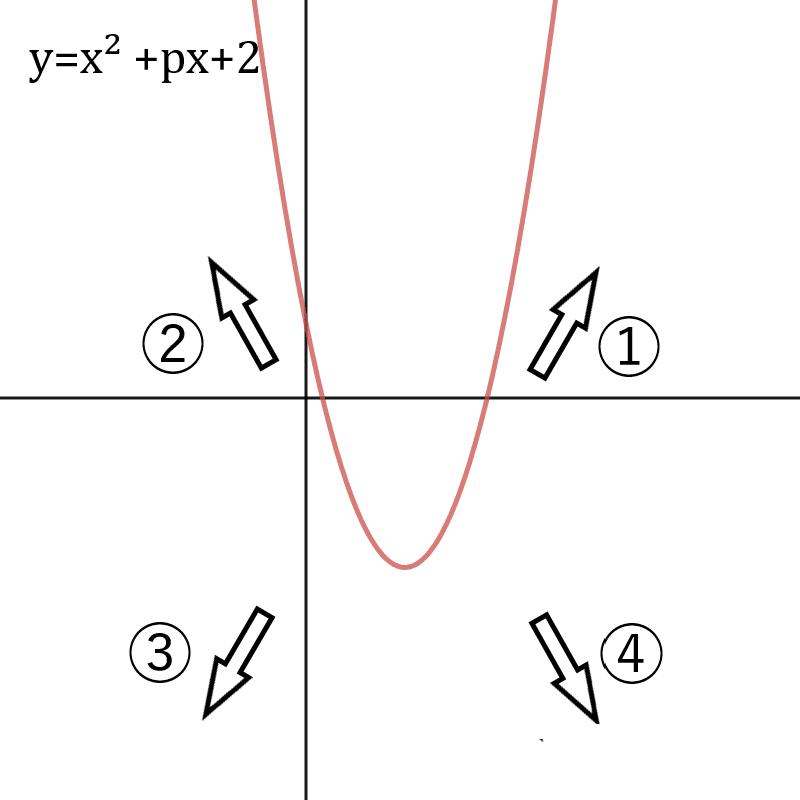
【問】y = x² + px + 2が上のようなグラフを与えられているとする(pは実数)。pの値を増加させたとき、最初にこのグラフが移動する方向として正しいものを①~④のうちから選べ。
さぁ、どうでしょう?レベル的には数学Iの2次関数までを履修している人であれば解くことができるように作ってあります。数学IIの図形と方程式の「軌跡と領域」の知識はなくても解けます。
受験生の皆さんは目安2分ぐらいで解答してみましょう。2次関数が苦手な方はどういう風に解けばいいのかじっくり考えてみましょう。
忙しい人は1,2,4だけ見てください!
1.解答と解説
さて、みなさん番号は選択しましたか?解答を発表しますよ?
|
|
|
正解は②です!どうでしょう、③と答えた人も結構いたのではないでしょうか?
想定していた解法を説明します。

そう、この問題には実は2つの「罠」が仕掛けられていたのです。
実際の動きが気になる方は↓のリンクよりDesmosでご覧ください
2.仕掛けられた2つの罠!
さて、この問題に仕掛けられた2つの罠、1つ目をかわすのは比較的簡単だったようですが、2つ目に引っかかる人が非常に多い印象です。
Twitterのアンケート機能を利用した結果、上記のようにばらけた結果を得られました。そして、③が多い!私の生徒数名に聞いた際も、③の選択肢を選ぶ生徒が非常に多かったです。
2つ目の罠をかわすのが難しい理由は複数考えられますが、最大の理由は「グラフと式の関係性を見抜けていない」ことにあるといえるでしょう。
グラフを見たときに
下に凸の放物線の軸が正の範囲にある
↓
y=x² +bx+ cにおけるbが負の数
↓
ということは、pは負の数
↓
pが増加するとき、p² は減少する
というような理解ができていなければなりません。③に引っかかった人の多くは、「pが増加するならば、p² も増加するんだから、y軸に関しては負の方向に進むのだろう」と考えたのではないでしょうか?
しかし、pが負の数の時は話が変わります。例えばpが-4からスタートしていた場合、pが-3,-2…と増加するにつれて、p² は9,4…と減少していってしまうのです。この罠を回避できた人が②の選択肢を選べるわけですね。
当然ですが、pに適当な数字(-4とか)を入れてちょっとずつpを増やしてみる!という方法が取れた人も罠を回避できます。案外この「とりあえず適当に代入して状況を確認する」ということができない人が多いですね~。
3.出題の意図
この問題は、共通テストに照準を合わせて個人で作成したものです。もしかしたら、大手予備校や塾等で似たような出題がされているかもしれません。
経験上数学が苦手な生徒はグラフの重要性を理解できていないことが多く、そもそもグラフを書かない生徒が多いです。しかし、グラフと式の関係を見抜けるようになりさえすれば、学校の先生や教科書が言っていることを理解できるようになるはずです。そのあたりにアプローチするための1問として用意しました。
また、共通テストについて、平成29年度の試行調査・数学IAでグラフ表示ソフトを用いた出題がされています(このリンクより、大学入試センターの試行調査問題に飛びます)。今まで(センター試験)は計算方法さえしっかり理解or猛練習できていれば、大抵の2次関数の問題は突破できる人が多かったですが、このような出題ではそうもいきません。
センター試験から共通テストへと移行する今こそ、「グラフと式を絡めて問題に取り組むことができる」能力を鍛えていくべきです。
4.グラフを理解して数学苦手を克服したい?
さて、この夏自分の苦手をつぶしたいみなさん、朗報です!数学が苦手な人のために、数学が苦手になる理由ランキング第1位といっても過言ではない「関数」についての特訓講座をNoSchoolで開講しております。
この講座は、10月までの限定講座で1コマ1時間、全6回の授業でひたすら「関数とグラフ」について学んでいきます。授業は基本的に「説明」がメインではなく、こちらの「問いかけ」を生徒に考えてもらい、一緒に答えを探すような構成をとっています。
無料体験も行っておりますので、是非お申し込みください!
【数学】夏の関数マスターコース【全6回】